In sports betting, “sample size” refers to the volume of data used for analysis.
Drawing conclusions from a small and insignificant sample may provide short-term insights, but it fails to accurately predict long-term success.
Increasing the sample size enhances the precision and reliability of evaluating the profitability of a betting strategy.
Article Contents
Sample Size In Betting
In sports betting, analysing historical or “past data” is pivotal for making informed estimates and uncovering patterns.
Take, for example, investigating whether a football league exhibits a home advantage. While it’s intuitive to assume that over a large dataset, the home team would demonstrate a clear advantage, drawing conclusions from a small sample can be misleading.
Put simply, the size of the dataset directly impacts the accuracy and confidence level of your estimates. A larger dataset not only bolsters confidence but also reduces uncertainty in your analysis.
In the following sections of this article, I employ a “test strategy” involving real horse racing odds to underscore the significance of selecting an appropriate sample size. The central question I aim to address is: what is the estimated long-term yield (ROI) of the bet selection method?
By using historical data to estimate the yield, my objective is to ascertain, with confidence, the profitability of the strategy and determine the expected return on investment (ROI) moving forward.
The Uncertainty of a Small Sample Size
Deciding on what constitutes a “small” or “large” sample size is challenging. There is no definitive number that can be used for every situation. However, when in doubt, remember that the optimal approach is to simply gather as much data as possible.
Now, let’s delve into the initial results of the test strategy, which demonstrated exceptional performance during its first 15 days.
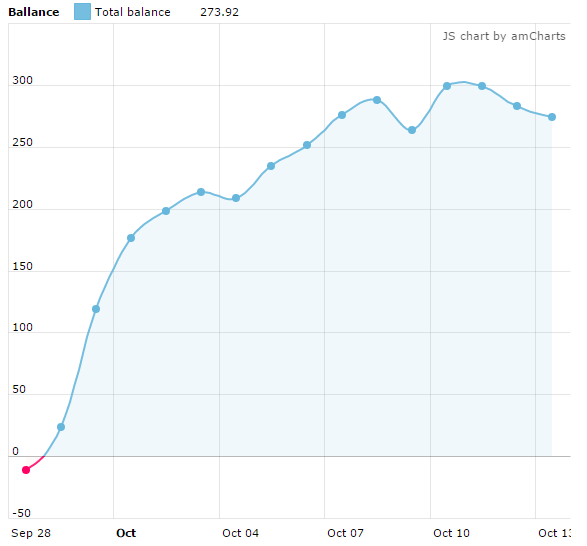
- Bets: 2,375 bets
- Average odds: 9.95 average odds
- Yield: +5.77%
With a yield of +5.77% and the upward trend depicted in the graph, there’s promise in these findings, especially given the total of 2,375 bets placed. That’s a significant sample size for potential future predictions, right?
Here's where I must issue a warning: assuming profitability based on past results can be dangerous in sports betting analysis. Samples may not accurately represent future outcomes!
This point will be reinforced in the subsequent section on ‘Large Sample Sizes’.
Uncertainties
Despite the seemingly large sample, there is a level of uncertainty surrounding the estimated yield (ROI) obtained from the first 15 days of the betting strategy. It’s imperative to also take into account the quality and variability of the data.
Greater variability within a sample typically leads to increased uncertainty in estimations. This is because “variability” implies that there is more diversity or inconsistency within the data points. This makes it harder to predict future outcomes or draw conclusions with confidence.
In this case, several factors warrant consideration:
- Was the bet selection method entirely impartial?
- Can the initial 15 consecutive days be considered representative of the entire year?
- Is the observed success rate indicative of typical performance, or merely a fortunate run of form?
- Do the average odds, standing at 9.95, potentially contribute to significant fluctuations in results?
- Have external factors such as weather conditions affected the outcomes positively or negatively?
While I remain confident in the fairness of the selection method, other uncertainties, such as those raised above, could have influenced the winning streak observed during the first 15 days of the strategy — especially the relatively high average odds of 9.95. In other words, it’s plausible that these results are merely on the “right side of variance“.
While it may seem skeptical to scrutinise a winning streak, in sports betting it’s imperative to maintain a critical approach towards analyses and to continue with data collection. After all, naive assumptions can lead to significant financial losses when placing real-stake wagers.
Remember: larger sample sizes improve the accuracy of estimations and minimise uncertainty. Now, on that note, let’s see what occurred as more data was gathered.
The Importance of a Large Sample Size
As previously hinted, the test strategy experiences a downturn despite its initially promising performance. This shift became apparent as data collection continued under identical conditions, resulting in a total sample size of 17,717 bets at £2 each.
The following graph integrates both the initial 2,375 bets and the expanded dataset.
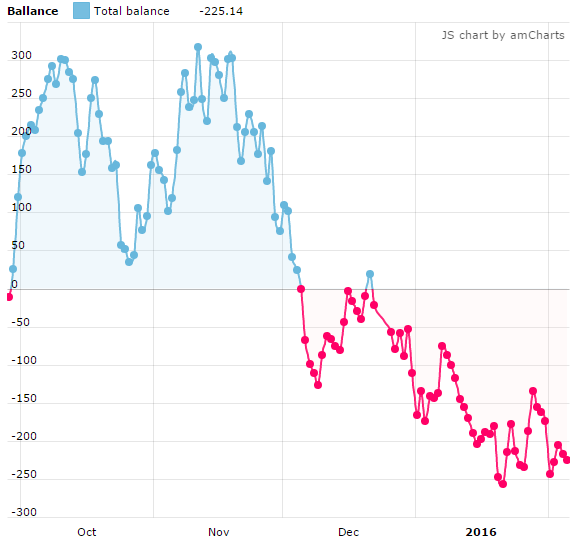
- Bets: 17,717
- Average Odds: 9.9
- Yield: -0.63%
With the expanded sample size, the precision of estimates is improved. Assumptions drawn from the smaller dataset are now somewhat invalidated.
Significantly, the yield (ROI) settles at -0.63% and the inconsistency in the graph offers little reason to believe that this selection method is profitable.
In theory, if we could extend this sample to infinity and include every future bet, we would attain the most accurate estimate for the value we seek—the yield of the strategy. However, this is an impossibility.
Nevertheless, this sample size of over 17,000 bets provides ample data for making informed decisions about the selection method: based on my experience in betting, I would not be eager to adopt this betting strategy!
More Uncertainties
Despite the clear indication that this strategy is not profitable, there are other uncertainties to consider:
- Was there a significant change that halted the continuation of the early positive results?
- Did competitors on the betting exchange adapt their strategies in response to mine?
While my strategy operated under consistent conditions over an extended period, it’s likely that the initial results were merely fortuitous, and the ROI eventually stabilised around its true value — approximately 0%. However, it’s also plausible that other traders detected patterns within the markets, potentially shifting the advantage in their favour.
Truthfully, it’s hard to know what occurred. In these types of scenarios, it’s crucial to scrutinise every aspect of your approach to identify any factors that may have influenced the change in results.
For Advanced Bettors: Power & Effect Size
In sports betting analysis, the concept of sample size plays a fundamental role in drawing meaningful conclusions from data. However, alongside sample size, it’s also worth considering the advanced methods of statistical power and effect size to ensure the reliability and significance of findings.
Statistical Power
Statistical power refers to the likelihood of detecting a true effect or difference in data analysis.
In the context of sports betting, statistical power helps assess the sensitivity of a study to detect significant patterns or trends in betting data.
A study with high statistical power has a greater chance of identifying meaningful effects, while a study with low power may fail to detect important relationships.
Effect Size
Effect size measures the magnitude of a relationship or difference observed in data analysis, providing a standardised measure of the strength of an effect.
In sports betting analysis, effect size helps evaluate the practical significance of observed trends or patterns, independent of sample size.
By quantifying the magnitude of effects, effect size allows analysts to assess the real-world impact of betting strategies or factors influencing betting outcomes.
Understanding statistical power and effect size in sports betting analysis is crucial for determining sample sizes, interpreting results, and conducting meta-analyses.
Final Thoughts
In sports betting analysis, selecting the right sample size is crucial for making accurate predictions.
Large sample sizes give more reliable analyses with greater precision and power, but it takes more time and effort. Therefore, automating data collection, using sources of available data, and investing in sports betting analytics tools is essential for making the most accurate predictions and assumptions possible.
In conclusion, the key takeaway is this: to develop and execute effective strategies, it’s crucial to gather and analyse substantial amounts of data. This assertion is only validated by the rise and fall of my test strategy.
- Best Horse Racing Tipsters |Top 40 Racing Tipster Services - April 24, 2024
- How To Resolve Disputes With Casinos & Bookmakers (Step-by-Step) - April 23, 2024
- Unibet Review | Bookmaker Rating & Signup Offer 2024 - April 22, 2024
Big swing in the results there!! Bit gutting when something seems to work and make money, then tails off. I suppose that’s the reality of betting. Thanks for sharing.
Found this from twitter…Good post. Seems that becoming a pro gambler is harder than you’d think
Did something change in your strategy?
Were you too obvious about what you were doing?
I find it hard to believe it would start losing money after so many bets
No, nothing changed in the strategy. I’ve always thought to myself that it was unusual how a strategy could work so well and then eventually lose. I have some ideas on why this may have happened. Perhaps there are bots that can identify patterns – such as other strategies…
I’ll write a post on my ideas on this.
Worth pointing out that a simple t-test on the data after the initial 2375 events would give you a confidence level of 82.04%, ie nowhere near significant enough to run with it. As a general rule, the higher your average odds are, the more bets you will need to establish significant confidence.